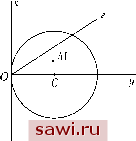ом, направленным по касательной в точке О и имеющим ту же силу, что и круговой ток.

Примем точку О за начало отсчета (рис. 32), касательную - за ось ж, диаметр ОС - за ось у. Тогда точка М будет находиться в плоскости yz.

Пусть сила тока равна единице; ds - элемент тока, dx - его проекция на ось Ох, г - расстояние от ds до точки М:

Рис. 32

dx г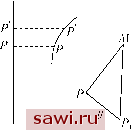

Необходимо проинтегрировать в пределах от -R до -\-R, где R - радиус окружности.

Пусть РР = ds, а Pi Pi = dx - проекция РР на ось X (рис. 33), равная dx, ri - расстояние от PiP/ до М. Векторный потенциал, порожденный прямолинейным током, выражается следующим образом:

Рис. 33

Этот интеграл необходимо проинтегрировать в пределах от -оо до +00. Однако, поскольку мы хотим изучить только порядок величины Pi, то можно рассмотреть ее в пределах от -R и -\-R.

Действительно, элементы, расположенные на конечном расстоянии от М, дают в выражении Pi конечные вклады, которыми можно пренебречь по сравнению с очень большими членами, заданными элементами, близкими к М.

В результате запишем

Можно найти верхний предел этого интеграла. Действительно, пусть

О, Уо, Zq координаты точек М, X, у, о координаты точек Р, X, О, О координаты точек Pi.

1 J г ri

ri - г

меньше, чем

Поскольку Г1 - г < у, получаем:

1 J

г Г1

р JP f , f ydx

Справедливы равенства

У dx откуда

Г ydx Г J г ~ J X

Когда точка Р бесконечно приближается к нулю, отношение

стремится к конечному пределу 2R, где R - радиус окружности. Та-

/* vt dx f xi dx

ким образом, интегралы / -- и / -- остаются конечными, следо-

вательно, разность F - Fi является конечной.

129. Порядок величины векторного потенциала. Поскольку разность Fi - F конечная, мы можем заменить круговую трубку на прямолинейную трубку с целью нахождения порядка величины векторного потенциала.

Сначала предположим, что речь идет о единственной трубке и что вихрь постоянен. Прямолинейная трубка будет цилиндром с круговым сечением, а векторный потенциал будет равен потенциалу притягивающей массы, распределенной по цилиндру, с плотностью

В треугольнике MPPi можно ввести следующие обозначения МР = г, MPi=ri, PPi=y.

Соотношение

+ с = -C/3olog/3o,

C = Cpl{l-logpo).

Предположим, что момент трубки (ро конечный. Если ро очень мал, то векторный потенциал будет иметь порядок величины log/зо.

Пусть ро - радиус цилиндра. Точку, расстояние р от которой до оси больше, чем ро, назовем внешней. Во внешней точке потенциал будет таким же, как если бы вся притягивающая масса была сконцентрирована на оси с плотностью

Потенциал в такой точке будет иметь вид

Cpllogp (р>ро). (3)

Для точки внутри цилиндра, т. е. при р < ро потенциал получается разложением цилиндра на две части путем проведения через рассматриваемую точку цилиндрической поверхности, которая имеет ту же ось, что и цилиндр. Внешний кольцевой слой не действует на точку, а другая часть производит то же действие, как если бы вся масса была сконцентрирована на его оси.

Следовательно, притяжение равно

для р>ро,

-СРо для р = Ро, -Ср для р < Ро.

Таким образом, потенциал будет выражаться

+ (4)

Значение потенциалов (3) и (4) должны совпадать при р = ро. Из этого условия определяем константу С: