8. Теорема Стокса. Для дальнейшего преобразования теоремы Гельмгольца применим теорему Стокса, предварительно напомнив ее читателю.

Пусть имеется замкнутая кривая С. Эта кривая лежит на некоторой поверхности и ограничивает на ней некоторую площадь А. Пусть duj - элемент этой площади-, I, т, п - направляющие косинусы нормали к duj. Теорема Стокса утверждает, что

{и dx -\- V dy -\- W dz) =

J I \dy dz/ \dz dxJ \dx dyJ

(10)

где первый интеграл берется по всем элементам кривой С; второй - по всем элементам duj площади А.

1°. Предположим сначала, что площадь А - плоская и располагается, например, в плоскости (ж, у). В этом случае:

/ = ш = О, п = 1, dz = О, duj = dx dy,

а поэтому

Это - известная теорема анализа. То же самое будет и в двух других координатных плоскостях.

2°. Площадь А является плоской, но расположенной в некоторой произвольной плоскости.

Пусть три бесконечно малых отрезка OA, OB, ОС (рис. 3) параллельны осям. Соединим точки А, В, С; они образуют бесконечно малый треугольник ABC. Наша теорема справедлива для этого треугольника. Действительно,

I-hhl-

АБСА АВОА ВСОВ САОС

Рис. 3

При этом стороны OA, OB, ОС дважды пробегаются в противоположных направлениях, в правой части остаются интегралы, взятые

(udx + vdy + W dz) =

= А0В( - ) +А0С(§! - ) +ВОС( - ф!).

\ау dz) \dz dx J \dx dy J

Треугольники АОВ, AOC, BOC являются ни чем иным как проекцией треугольника ABC на координатные плоскости. Таким образом, если обозначить

ABC = duo, АОВ = / duo, AOC = ш duo, BOC = n duo, TO будем иметь:

j udx + vdy + wdz = j ldw[-f+...

Теперь теорема доказана в общей постановке, так как произвольная площадь может быть разложена на достаточно маленькие треугольники, подобные ABC.

В своем известном трактате Максвелл часто пользовался этой теоремой.

9. Замечания Гельмгольца. Определение вихря. Гельмгольц ввел следующие величины

dw dv du dw г. dv du ч

dy dz ~ dz dx ~ dz dy ~

в этом случае, согласно формуле Стокса, имеем:

J {udx + vdy + W dz) - J duj{l + mr] + n().

Согласно установленному нами уравнению (6), этот интеграл, взятый по площади А, постоянен при движении этой площади.

вдоль АВ, ВС, С А, как и в левой части. Исходя из того, что треугольники АОВ и т.д. бесконечно малые, и прилагая к каждому из этих треугольников, лежащих в координатных плоскостях, равенство (1), получим: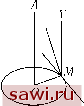

J = J ipR duj.

Пусть ifo - средняя угловая скорость движения по окружности, определенная формулой

(fdu; = 27г(о-

Отсюда

J = 2KoR.

С другой стороны, известно, что для того, чтобы получить элемент интеграла J, необходимо умножить элемент duo площади А на два и на

Tourbillion (франц.) - Прим. ред.

Вектор, имеющий компоненты (, т/, Гельм-гольц назвал вихрем (завихренностью). Этот термин требует некоторых пояснений.

Предположим, что кривая С является окружностью (рис. 4). Через точку М на этой кривой проведем вектор MV, который представляет собой скорость с составляющими {и, V, w). Выражение

udx -\-V dy -\-W dz р

представляет произведение элемента кривой ММ на проекцию скорости в направлении ММ. Это произведение представляет собой работу, которую дала бы сила, численно равная скорости, когда ее точка приложения переместилась бы из М в М. Интеграл J равен работе, которую произвела бы эта сила, если бы точка М описывала всю окружность.

Разложим вектор MV на три другие, первый из которых параллелен оси OA, перпендикулярной плоскости круга, второй направлен по касательной к кругу в точке М и, наконец, третий - по радиус-вектору ОМ. Работа при этом будет произведена только касательной компонентой. Представим эту компоненту в виде cpR, где ср является угловой скоростью, R - радиусом круга. Если положить

= icosct;, у = Rsinu;,

то получим