146. Пусть имеется однородная жидкость, свободная поверхность которой находится под давлением атмосферы. Если через р обозначим избыток действительного давления по отношению к атмосферному давлению, то в уравнении (5) необходимо положить

р = 0,

что приводит к

Ф = -gz, (8)

где ф - функция от г, а это и есть уравнение свободной поверхности жидкости.

Предположим, что существует только одна вихревая трубка, имеющая форму кругового цилиндра с осью Oz. Вихрь постоянен внутри этого цилиндра и равен нулю снаружи. При этом цилиндр будет иметь равномерное вращательное движение.

Пусть Го - радиус цилиндра. Внутри его поверхности, т.е. при г < Го, скорость пропорциональна г и

Т = аг\

Снаружи, при г > Го, имеется функция скоростей и

гр

Эти два выражения для Т должны иметь одинаковое значение на поверхности цилиндра, т.е. при г = го. Следовательно,

гуг - аго - -,

откуда

а = агд.

При помощи этих соотношений вычислим значения ф. Внутри цилиндра, как известно,

ф -\-Т = const,

поэтому

ф = -аг + с;

а снаружи

ф - Т = const, значит, .

Эти формулы должны привести к одному значению при г = го-Таким образом,

-аг1 + С= + С,

что задает соотношение между постоянными С и С .

Постоянную С можно считать произвольной. Изменить ее значение - все равно, что переместить плоскость ху параллельно самой себе, это приведет к тому, что к 2:, а следовательно, и к ф, просто добавится постоянная. Пусть С = 0. При этом выборе для г = оо имеем

= 0,

а также

z = 0.

Таким образом, свободная поверхность жидкости может рассматриваться как асимптотическая плоскость. Именно эта плоскость выбрана в качестве ху, она является уровнем жидкости, расположенным

на очень большом расстоянии от оси.

Следовательно, уравнение свободной поверхности относительно к оси вращения и асимптотической плоскости будет иметь вид:

1° внутри вихревой трубки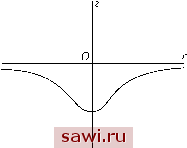

2° вне этой трубки

Рис. 42

gz = --

(10)

Первое уравнение представляет собой параболоид: внутри трубки меридианным сечением свободной поверхности будет маленькая дуга параболы.

Второе уравнение представляет собой поверхность, меридианное сечение которой образуется двумя асимптотическими ветвями к оси г (рис. 42). Две кривые соединяются на сечении вихревой трубки.

Отметим, что z всегда отрицательна. Поэтому свободная поверхность целиком расположена ниже плоскости ху.

Это обстоятельство не зависит от частных гипотез, которые введены нами ранее. Это - общий случай, что мы сейчас и покажем.

Действительно, функция ф равна нулю при г = оо. Следовательно, справедливо равенство

ф

+ 00

Поскольку Т и г обязательно положительны, то это будет выполняться и для ф. Следовательно, z, согласно уравнению (8), будет отрицательной.

Этот результат не соответствует наблюдениям. Действительно, все, кто имел возможность наблюдать смерчи, утверждают, что жидкость, наоборот, поднимается к центру вихря так, что она образует нечто вроде утолщения под свободной поверхностью. Это разногласие между вычислениями и наблюдениями, вероятно, частично связано с тем, что в нашем вычислении мы предполагали равномерное распределение давления на поверхность жидкости. Это условие, по-видимому, не выполняется в случае со смерчем. Однако сомнительно, чтобы эта гипотеза имела достаточно большое влияние на результат вычислений и устранила отмеченную нами трудность.

147. Распределение давления в газе. Если движущаяся среда является газом, то мы можем определить его состояние, предполагая, что давление р меняется в плоскости, параллельной плоскости ху. Если газ сохраняет постоянную температуру, то необходимо воспользоваться формулой (6), и тогда в плоскости z = zq имеем

Inp = -/3gzo - /Зф.

Значение ф становится равным нулю на бесконечности. Пусть ро - соответствующее значение р, тогда:

Inpo = -l3gzo

Второй член является отрицательным, поскольку ф всегда положительно, как мы только что показали. Следовательно, отношение меньше единицы, и, значит, внутри вихря имеется область пониженного давления.

Если газ подвергается адиабатическому изменению, то лучше воспользоваться формулой (7). В плоскости z = zq давление р будет иметь