(о = / / е~ F{x, у) da df3 = F{x, у) е~ da df3.

Так как +/3

то уравнение

е h dad/3

Со = Fix, у)

и определит функцию F.

Если начальное значение ( зависит только от г, то F также зависит только от г и можно будет определить ( в некоторый момент времени, при условии, что не нарушена симметрия или условия устойчивости выполняются.

158. Теорема Гельмгольца для относительного движения.

Теорема Гельмгольца показывает, что интеграл

и dx -\- V dy -\- W dz

является постоянным при наличии силовой функции. В случае относительного движения силовая функция отсутствует, и теорема более не справедлива.

Как мы знаем, имеем выражение

dt j

= diP + dT,

d = dV- ,

когда существует потенциал V.

Для того чтобы отождествить это уравнение с уравнением (12), нам достаточно положить

где К обязательно положительна.

Далее, принимая гу

можно будет вычислить ( для любого момента времени.

Для того чтобы найти функцию F, необходимо определить значение С в начальный момент времени, то есть при f = О

= 2а;о J{v dx - и dy).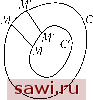

Пусть С - кривая интегрирования. Спроецируем ее на плоскость ху. Пусть А - площадь, ограни- Рис. 43 ченная этой проекцией (рис. 43), а М и М - две бесконечно близкие точки. Тогда проекциями ММ на три оси будут отрезки dx, dy, dz. За время dt частицы, находящиеся на кривой С, перейдут на кривую С и, в частности, точка М перейдет в точку Mi, а М в М{. Проекциями MMi являются отрезки udt, vdt, wdt. Четырехугольник MMMiM{ подобен параллелограмму, проекция которого на плоскость ху ограничивает площадь, равную

dt{v dx - udy).

Таким образом, интеграл

dt J {vdx - и dy)

представляет собой изменение dt площади А за время dt. Следовательно, получим соотношение:

dt dt

J = 2uJoA + const.

Таким образом, если Jq и Aq - начальные значения J и А, то получаем Jo = 2uJoAo + const, J - Jq = 2uJo{A - Aq).

Если же потенциал больше не существует, то аналогичное выражение имеет вид , di; = Xdx + Ydy + Zdz- .

Если переносное движение является, к примеру, вращением вокруг земной оси с угловой скоростью ujq, то получим

X dx -\-Y dy -\- Z dz = dV -\-2u;o{vdx - и dy),

согласно теореме Кориолиса, понимая под потенциалом V обычную центробежную силу, при этом ось z является осью вращения. В результате получаем выражение

= J(dV + dT) + j 2u;o{vdx -udy).

Первый интеграл равен нулю и поэтому dJ

Рис. 44

Пусть имеется окружность радиуса го (рис. 44). Частицы, находящиеся на этой окружности, первоначально находятся в состоянии равновесия относительно земной поверхности. Следовательно,

0 = тгго sin Л,

где Л является широтой и

Jo = 0.

Если происходит возмущение (например, воздушная тяга к центру окружности), то частицы через некоторое время займут замкнутую кривую, подобную окружности радиуса г. В этом новом положении получим следующие соотношения

А = 7гг sin л,

J = 2а;о7г(г - Гд) sin Л.

Пусть имеется вращение, а о; - его угловая скорость или вертикальная составляющая вихря. Вычисляя интеграл

со da,

где da - элемент поверхности при условии, что cj является постоянной, получим

J = 2и; J da = 2а;7гг Приравнивая два выражения для J, находим

со = ujo sinAl -

Если отношение достаточно мало, то и; станет очень большой и всегда будет иметь один и тот же знак, т.е. вращение всегда будет направлено в одну и ту же сторону.

Это и есть одно из объяснений образования атмосферных циклонов.