На развертке поверхности только кривые первого рода являются замкнутыми.

16. Момент вихревой трубки. Интеграл J, взятый вдоль замкнутой кривой первого рода, равен нулю (п. 12). Но доказательство не применимо непосредственно к кривым второго вида, и, следовательно, формулировка теоремы должна быть изменена следующим образом:

Теорема. Интеграл J, взятый вдоль замкнутой кривой второго рода, имеет одно и то же зна- jft чение, какой бы ни была эта кривая.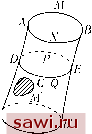

Действительно, пусть DPEQ и DPEQ - два замкнутых контура: необходимо показать, что

JdPEQ - J DPEQ

Возьмем точку Р на первой кривой, точку Р - на второй и соединим их между собой РР (рис. 7). Контур

PEQDP - РР - PDQEP - РР

может быть рассмотрен как замкнутый контур первого рода. Таким образом, вдоль этого контура интеграл J равен нулю, другими словами:

Рис. 6

PEQDP

-\- Jpp/ -\- Jр/ г>0 К р ~\~ Jр р - 0.

PDQEP

Второй и четвертый интегралы взаимно уничтожаются, так как отрезок РР дважды пробегается в противоположных направлениях. Таким образом, получим

JpEQDP + JpDQEP - о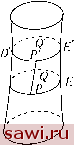

Рис. 7

JpEQDP - JpEQDP

Определенный таким образом интеграл J называется моментом вихревой трубки. Этот момент остается постоянным, в то время как частицы, расположенные в трубке, могут перемещаться.

17. Применение. Бесконечно тонкие вихревые трубки. Рассмотрим бесконечно тонкую вихревую трубку (рис. 8). Проведем прямое сечение этой трубки (являющейся замкнутой кривой второго рода). Таким образом, можно вычислить момент трубки, взяв интеграл J вдоль этого сечения. Его значение, как следует из п. 9, равно

Рис. 8

где является нормальной составляющей вихря. В рассматриваемом случае

J = 2duj,

так как вектор вихря перпендикулярен выбранному элементу площади duj (прямое сечение, которое всегда можно положить параллельным плоскости yz). Теперь можно заключить, что:

Произведение перпендикулярного сечения бесконечно тонкой вихревой трубки на вихрь постоянно вдоль трубки. Это произведение остается также постоянным в любой момент времени.

Эти два предположения немедленно следуют из того, что J постоянен при тех же условиях, что и п. 6. Они могут быть применены как к жидкостям, так и к газам, когда существует функция, обозначенная ранее через ф.

18. Теоремы, связанные с единственными жидкостями.

Пусть имеется бесконечно тонкая трубка тока (силовая трубка) и два перпендикулярных сечения, бесконечно близкие между собой в трубке. Объем трубки, заключенной между этими двумя сечениями (рис. 8), может быть рассмотрен как цилиндр, который имеет в качестве основания дифференциал площади duj, а в качестве высоты ММ, где М и М являются точками двух сечений, расположенных на одной и той же вихревой линии. Объем этого цилиндра равен

ММ duo.

В следующий момент времени частицы, которые составляли этот объем, образуют другую вихревую трубку. Частицы, которые занимали два перпендикулярных сечения, займут другие сечения, бесконечно

-dtTxWyWz

близкие первоначальным, которые не обязательно будут перпендикулярными. При этом уподобляемый цилиндру объем, заключенный между этими сечениями, будет равен

MiM[ duji,

где MiM[ - отрезок образующей, а duji - перпендикулярное сечение. Если речь идет о жидкости, то ее объем остается постоянным и

MMdu; = MiM[du;i.

Таким образом, очевидно, что duo меняется в обратно пропорциональной зависимости от вихря. При этом расстояние ММ между двумя частицами меняется пропорционально вихрю. Можно сказать, что ММ представляет собой по величине, направлению и смыслу величину вихря, умноженную на некоторую постоянную е.

Пусть X, у, Z - координаты точки М, а х -\- е, у -\- ег], z -\- еС - координаты точки М.

За бесконечно малый отрезок времени dt координаты точки М станут равными

X -\- udt, у -\- vdt, Z -\- wdt. Координаты точки М -

ж + + 11 ,... и т. д.

При этом

Таким образом, координаты точки М запишутся в виде

С другой стороны, учитывая, что проекции ММ равняются г, ег], гС, координаты этой точки имеют вид

xudte{idt. Приравнивая два эти выражения, получим