Если показатель степени b близок к единице, что имеет место при жестких обоймах и относительно больших углах заклинивания, то зависимость М = М можно принять линейной, т. е.

М = ftg. (114)

Тогда уравнение относительного движения обойм примет вид

(115)

2? Л1 - УИ

Период заклинивания у механизмов свободного хода импульсных вариаторов протекает при возрастании угловой скорости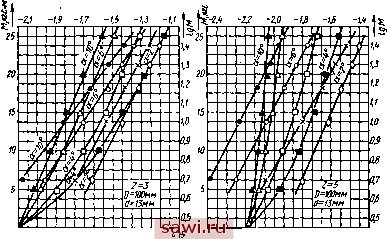

US Л5тЛЛ{Л5Л5.

i,pad

о IS 45 fib т215т

о,от Iuwi#zisiaa3fl6ft05 от тьтгтз

i,pad

Рис. 12

ведущей обоймы (о. Угловая скорость ведомой обоймы а в начальный момент заклинивания равна нулю (для вариаторов с одним или двумя механизмами свободного хода) (см. рис. 11 б,) либо имеет некоторую положительную величину (для вариаторов с тремя и больше механизмами свободного хода) (см. рис. И, б)..

В первом случае, когда заклинивание начинается при неподвижной ведомой обойме, в начале процесса заклинивания момент Ml больше момента М (5), действующего со стороны ведущей обоймы, эта фаза с периодом 1з (см. рис. 11, б) протекает при неподвижной ведомой обойме. Во второй фазе с периодом й на участке аЬ происходит ускоренное движение ведомой обоймы.

Рассмотрим возможные случаи заклинивания МСХ импульсных вариаторов и соответственно решения уравнения относительного движения обойм.

Заклинивание при Ml = Ml {t). Считая, что колеблющаяся обойма импульсного вариатора приводится в движение посредством преобразующего механизма, имеющего постоянную угловую скорость кривошипа ю, можно кривую изменения углового ускорения этой обоймы == {I) в период заклинивания (участок аЬ) аппроксимировать:

si = 81 cos тсок (46)

где т - постоянный коэффициент.

В каждом конкретном случае применения импульсных вариа-торовв приводе рабочих машин можно определить закон изменения моменту сил сопротивления:

Однако малая продолжительность периода заклинивания дает основание принять

MlMlokt, (117)

где Мсо - момент сил сопротивления в начальный момент заклинивания; k --постоянный коэффициент.

Используя последние два уравнения, а также уравнения (105)

и (113), получаем

= 81 cos rmj -f + с.

(118)

Данное нелинейное дифференциальное уравнение с постоянными коэффициентами можно решить приближенно численными методами посредством ЦЭВМ или нижеизложенным графическим методом в плоскости i,Ot.

Пользуясь начальными условиями

I (0) = О и Г(0) = О,

из уравнения (118) определяем

Далее найдем радиус кривизны интегральной кривой в началь-ной точке:

Так как в начальный мвмент (0) = О, то этим радиусом с центром в точке 0 проводим дугу Оа окружности (рис. 13) до

йе{5есечения с правой вертикалью Первого элеМейтарно?о участка Ati-

, Определив величины (Ai) и i(Ai), находим радиус кривизны из выражения

Pi- ГЩ)

й проводим этим радиусом из центра 0, лежащего на направлении линии Оа, отрезок аЬ круга кривизны до вертикали следующего участка А/j. Аналогичным способом выполняем построение на других участках интервала t. С целью увеличения точности можно применить метод добавочного полушага.

Учитывая то обстоятельство, что в конечный момент заклинивания относительная угловая скорость обойм равна нулю, из построенного графика (рис. 13) определяем время заклинивания 4 и наибольший угол относительного поворота обойм иах- По величине угла ах на основании уравнения (111) найдем максимальный момент, действующий на механизм: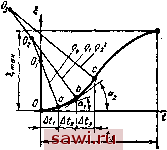

Рис. 13

(120)

По величине этого момента следует производить расчет на контактную прочность и жесткость механизмов свободного хода.

При линейной характеристике жесткости механизма уравнение относительного движения обойм в период заклинивания на основании уравнения (118) будет представлять линейное неоднородное дифференциальное уравнение с постоянными коэффициентами .

I + ail = 8ix:os m(x)t -{-qt-\-c, где

(121)

Решение данного уравнения имеет вид I =-Ч-2-cosmoaj + -t--X

xl/l+ctg4oCos(/5- cfo)-\-~y

(122)

af/2

Заклинивание при постоянных моментах сил Движущих и сил сопротивления. Уравнение (113) в этом случае будет, иметь вид

©ico = (аз - ЛЯ*) dl.

где

2 =

-г--\--r-

интегрируя выражение (123), получим

= l,4l/ .5 5-

(124)

Так как в конечный момент заклинивания (о - О, g - Ux. то из последнего выражения найдем

>шах

аг (6+1) AJ

(125)

Используя формулу (111), получим величину максимального момента

Мшях = -1-

(126)

Время периода заклинивания можно определить из уравйения (124):

dl - (127)

После преобразований и подстановки

Smax

соотношение (127) можно записать в виде

± 1

Uax dx

(128) 201

или через гамма-функции

Согласно формуле Лежандра запишем

Ш(+4)-(4).

Используя это выражение и зная, что Г (±.) = я, искомый , интеграл можно представил-ь в форме

пачспис Sn,ax ИЗ (15) В следующем виде:

3 - ~3£Г2-fiirr

2 2* 2* г

(129)

прим?т\иГ Р-Ристике жесткости уравнение (111)

(Odco = ( 3 rf

или после интегрирования

Так как при со = 0; I =

(130)

вшах

бшах 202

202

м - м

- + -7

2 I

Подставляя Imax В уравнение (114), найдем максимальную Величину момента:

Jmax- J \ 4-

Из выражения (130) определим

VkJ \ 2

arcsin

(131)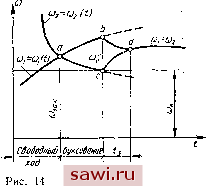

Ударное заклинивание. При некоторых режимах работы процесс заклинивания протекает при ударном воздействии сил на ролики и обоймы МСХ. Кроме того, ударное заклинивание МСХ возможно у вариаторов, установленных в приводах машин с ударным приложением нагрузки на рабочем органе (прерывистое точение на токарных станках, пульсирующие конвейеры, машины горной промышленности и т. д.). Ударное заклинивание возможно и при плавно изменяющихся нагрузках, если прижимные усилия не обеспечивают контакт в начальный момент заклинивания, когда угловые скорости обойм выравниваются, а контакт ролика с обоймами наступает при относительной :корости обойм, направленной в сторону заклинивания механизма.

Нарушение контакта роликов с одной из обойм может произойти:

из-за наличия слоя смазки, разделяющего контактные поверхности, что возможно при высокой вязкости смазывающей жидкости, а также расклинивающем воздействии смазывающего слоя при вращении цилиндрических роликов или перемещении эксцентриковых роликов с кольцевой прижимной пружиной относительно одной из обойм (чаще всего относительно внутренней обоймы);

в результате динамических усилий, действующих на ролик и стремящихся оторвать его от одной из обойм.

Чтобы представить удар1ое заклинивание при отсутствии контакта роликов с одной,из обойм, обратимся к рис. 14. Если