ЛЕКЦИЯ 6 ОСНОВНЫЕ ПОСТУЛАТЫ

В предыдущих лекциях были изучены характеристики кинематики и деформирования сплошной среды и дано определение её движения. Правда, под такое определение подходит и движение нематериальной среды (например, тени). Материальность среды задаётся плотностью вещества. Каждой частице приписывается положительный скаляр р{СЛ)- Тогда масса т некоторого объёма V определяется интегралом

т= pdV. (6.1)

Для объяснения причин возникновения движения материальных тел требуется введение понятия силы. Едва ли во всех естественных науках есть более распространённое и менее поддающееся определению понятие. Поэтому не будем останавливаться на нём подробно, а предположим, что читатель уже немного знаком со вторым законом Ньютона из классической механики. Заметим только, что Герц сформулировал все законы механики, вовсе не используя понятие силы. К сожалению, механика Герца не получила широкого распространения. В МСС силы делятся на массовые и поверхностные (иногда вместо массовых сил используют объёмные силы). С помощью этих понятий можно сформулировать основные постулаты механики сплошной среды.

Прежде чем переходить к их формулировкам, докажем ряд вспомогательных лемм, имеющих, впрочем, и самостоятельное значение.

Основная лемма. Пусть G и V - произвольная подобласть G. Функция /(xi,Х2,хз,t) непрерывна в G и обладает свойством

f{xuX2,xs,t)dV = 0 (6.2)

для любого момента времени t. Тогда / = 0.

< Доказательство проведём от противного, а именно: предположим, что в G существует точка (х1,Х2,хз), такая что /(х1,Х2,хз, t) ф О (для определённости /(хь Х2, хз, t) > 0). В силу непрерывности / существует шар Ш£(х1,Х2,хз) радиуса е с центром в (х1,Х2,хз), который полностью принадлежит С и в котором f а > 0.

Выберем V = и, используя свойства определённого интеграла, запишем

/с1Уа\Ше\ = 7гае>0, (6.3)

ЧТО противоречит условию (6.2) леммы. Следовательно, наше предположение о наличии в G хотя бы одной точки (х1,Х2,хз), где /(xi,X2,X3,t) 7 О, неверно. Основная лемма доказана. ►

Назовём жидким, или подвижным, объёмом меняющуюся со временем область пространства, состоящую из одних и тех же материальных частиц.

Лемма о дифференцировании по времени интеграла по жидкому объёму. Пусть V - жидкий объём. Тогда

fdV =

+ /divf) dV, (6.4)

где f{x\,X2,x,t) = f{x,t) - любая функция, для которой существуют обе части равенства (6.4).

Ч В момент времени t жидкий объём занимал область V в пространстве, а в близкий к t момент t + At область = V + AV. При этом AV, как видно из рис 22, состоит из элементарных цилиндрических объёмов dV таких, что

dV = di:vnAt, (6.5)

где dTi - элемент поверхности V, являющийся основанием цилиндра dV, г v - nAt - высота dV. 22

Обозначим левую часть (6.4) через I{t). Согласно определению производной функции одного переменного и формуле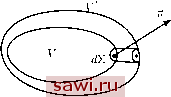

Остроградского-Гаусса (2.43) 1

I{t) = lim

= lim

AtO At

+ lim

AtO At

fix, t + At) dV -fix, t + At) dV -fix, t + At) dV =

fix,t)dV

fix,t)dV df

ix, t) dV +

fix,t)v-ndT, =

+ div ifv) dV. (6.6)

Заметим теперь, что

I + 4iv(/?) = % + lv, + /dIv J= f + /divft (67)

Из (6.6) и (6.7) следует утверждение (6.4) леммы. Из доказательства следует, что / может быть не только скаляром, но иметь также векторную либо тензорную природу. ►

Сформулируем первый постулат механики сплошной среды, который называется законом сохранения массы.

Закон сохранения массы (I постулат МСС). Пусть V - произвольный жидкий объём в R. Тогда в любой момент

времени

= 0,

(6.8)

где величина т определена в (6.1).

Простое и интуитивно понятное ( масса никуда не исчезает и ниоткуда не возникает ) равенство (6.8) представляет собой интегральную формулировку закона. Воспользуемся леммой о дифференцировании по времени интеграла по жидкому объёму (равенство (6.4)). Получим

pix, t) dV =

dp ,. - + pdiv.

(6.9)

Жидкий объём V произволен, поэтому основная лемма приводит к соотношению

- + pdwv = О в любой точке пространства и в любой момент времени.

(6.10)