В силу симметрии тензора Р все три корня: а\, а, сгз, уравнения (8.9), называемые главными напряжениями, действительны, а собственные направления, называемые главными направлениями, взаимно ортогональны. Выразим инварианты (8.10) через ai, сг2 и аз:

(8.11)

Инварианты симметричных тензоров второго ранга уже встречались в лекции 4, где говорилось о том, что любая функция F{I\, I2, Is) также является инвариантом. Поэтому вместо /2 часто используют и другие квадратичные инварианты, например а\ + а2+сг\, а вместо /3 - кубические инварианты, например + сг + сг (см. (4.53)).

Итак, на трёх взаимно перпендикулярных главных площадках, каждая из которых ортогональна своему главному направлению, касательные напряжения равны нулю. Такая тройка площадок существует в каждой точке среды и единственна, если с\Ф с-ф (УъФ cf\. Если, например, аФ сгз, то на любой площадке, содержащей третью главную ось, касательное напряжение нулевое. Если же ai = сг2 = аз, то тензор напряжений в данной точке явлется шаровым и т = О на любой площадке,

проходящей через эту точку.

Направим в некоторой точке О векторы ki ортонормирован-ного базиса вдоль главных осей. В этом базисе

г, = 5]аа5,г5. (8.12)

и согласно (8.3) компоненты вектора S имеют вид

= а ЛГ .

Рис. 30

(8.13)

Построим бесконечно малый октаэдр с центром в точке О (рис. 30) такой, чтобы нормали к каждой из восьми его граней имели компонентами числа ±l/\/3. Грани построенного октаэдра равнонаклонены к главным осям и называются октаэдрически-ми площадками. Вычислим на них нормальное а и касательное т напряжения. Согласно (8.13) и определениям (8.5)

и (8.6) имеем

= J2 Л* = (1 + + стз) = = а, (8.14)

= (1-2)2+ (а2-с7з)2+ (a3-ai)2 = /2 - З/2, (8.15)

так как НГ = ±1/л/3. Величина а называется средним напряжением. Как видно из (8.14) и (8.15), нормальное и касательное напряжения на октаэдрических площадках выражаются через инварианты (8.11) и, следовательно, сами являются инвариантами. Их можно выбирать в качестве линейного и квадратичного инвариантов тензора напряжений.

Поставим теперь вопрос: на каких площадках в данной точке касательное напряжение достигает своего максимального значения? Очевидно, что на этих же площадках достигает максимума и квадрат касательного напряжения. Исследование удобно проводить в главных осях, поэтому с учётом (8.13) формулу (8.6) можно записать следующим образом:

(,W)2 = 5(iV)2 (,(iV))2 2д,2 (jaNl). (8.16)

кроме того, компоненты единичного вектора нормали N\, N2, Щ связаны условием

Nf + Nl + Nl = 1. (8.17)

Составим функцию Лагранжа

/(ЛГьЛГ2,ЛГз) = (rW)2 - A(iV,iV, - 1) (8.18)

С неопределённым множителем Л и, используя (8.16), запишем необходимые условия экстремума:

-2XNa = 0, (8.19)

=l-iV.iV. = 0, где а = 1, 2, 3.

Система четырёх уравнений (8.19) удовлетворяется в нижеперечисленных случаях.

а) Лск = ±Ь Np = Nj = 0. три площадки с такими нормалями, как уже известно, являются главными. На них неотрицательная величина г\ действительно, принимает своё экстремальное, а именно минимальное (нулевое), значение.

6)Na = 0, NpO, NjO. Тогда система (8.19) сводится к трём уравнениям:

ap-2{apNl + aN)

= А, = А,

(8.20)

Предположим, что все главные напряжения различны, и расставим их в убывающем порядке:

ai > 2 > СГ3. (8.21)

В этом случае решение системы (8.20) следующее:

Щ = Щ=1/2, (А7) = {(1;2),(2;3),(3;1)}. (8.22)

Итак, необходимые требования условного экстремума, сформулированные в пункте (б), реализуются на шести различных площадках, одна из компонент нормали к каждой из которых равна нулю, а две другие компоненты, как следует из (8.22),

равны ±l/\/2. Геометрически это означает, что все эти площадки являются биссекторными к всевозможным двугранным углам, образованным главными площадками. На рис. 31 показаны две из шести таких площадок, они являются биссекторными к двугранным углам, которые образуют первая и вторая главные площадки.

Подсчитаем, пользуясь (8.16), каждой из шести найденных площа-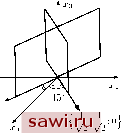

Рис. 31

(rW2

значения [т) на док. Заметим, что (т) зависит лишь от квадратов компонент нормали, поэтому эти шесть площадок разбиваются на три пары с нормалями {О, 1 /л/2 , =Ы/л/2}, {1 /л/2, О, ±1/л/2}, {1/л/2, ±1/л/2, 0}. На ортогональных площадках из одной пары касательные напряжения совпадают. Углы же между двумя площадками из разных пар равны тг/З, так как косинусы углов между соответствующими нормалями равны ±1/2.