ЛЕКЦИЯ 2 ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА

Векторной линией данного векторного поля называется такая кривая, в каждой точке (х1,Х2,хз) которой её касается вектор а(х1,Х2,хз), принадлежащий этому векторному полю

а(ж1,Ж2,жз)

Рис. 7

(рис 7). Если a(xi, Х2, Хз, t) явно зависит от времени, то картина векторных линий будет со временем меняться. Для векторного поля скоростей векторные линии называются линиями тока.

Если через точку пространства проходит более одной линии тока, то эта точка называется особой. Примеры таких особых точек изображены на рис. 8. Проведём в момент времени t через некоторую неособую точку М с радиусом-вектором г линию тока (рис. 9). Вдоль этой линии выберем естественный параметр

Рис. 8

Рис. 9

отсчёта - длину дуги s. Тогда согласно определению линии тока

- = Ki7(xi,X2,X3,t),

(2.1)

где К, вообще говоря, зависит от s. Запишем соотношение покоординатно:

dxi = Kvi ds = Vi dX, Kds = dX, (2.2)

или в виде dx\

= dX, (2.3)

vi (Xi, X2, Хз, t) v2ixu X2, X3, t) Vs{xu X2, X3, t)

где параметр Л - скалярная функция длины дуги s.

Система трёх уравнений (2.3) определяет картину линий тока в пространстве в момент времени t. Отметим существенное различие между решениями этой системы и решениями системы (1.25), которую по аналогии с (2.3) запишем следующим образом:

dx, dx, dx, 2.4)

г!(xi, Х2, Хз, t) г2(х1, Х2, Хз, t) гз(х1, Х2, Хз, t)

Оно состоит в том, что в (2.3) время фиксировано и входит как параметр, а в (2.4) время меняется и представляет собой независимый аргумент.

Поскольку решением системы (2.3) является семейство линий тока, а решением системы (2.4) - семейство траекторий, то линии тока, вообще говоря, отличаются от траекторий частиц. В самом деле, пусть плоское тело представляет собой квадрат ABCD (рис. 10), двигающийся поступательно в своей плоскости, причём центр М квадрата вращается по окружности вокруг неподвижной точки О. Траекториями точек квадрата в данном случае будут окружности радиуса \0М\ (например, для точки А центр такой окружности находится в точке А). В силу же поступательности движения, т. е. равенства скоростей всех точек тела, линии тока в каждый момент времени будут представлять собой семейство отрезков.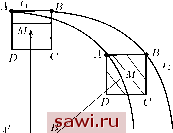

Рис. 10

atx\ + X2 atx2 - x\ 0 Из системы дифференциальных уравнений (2.5) следует, что линиями тока будут пересечения плоскостей хз = const и цилиндрических поверхностей, определяемых уравнением

dx2 atx2 - Xl dx\ atx\ + X2 * Для интегрирования уравнения (2.6) с помощью замены у{х) = Х2/Х1, X = х\ сведём его к уравнению с разделяющимися переменными,

y + at dx

которое имеет следующий интеграл:

х1 + 1/2 ехр (atarctgi/) = С. (2.8)

Переходя опять к переменным х\, Х2, запишем (2.8) в виде

J{xif + {x2fexp (atarctg] = С (2.9)

V \ X\J

или же в полярных координатах на плоскости OxiX2 (г = = \/(3:i)2 + (х2)2, = arctg(x2/xi)):

г = Се-, X3 = Ci. (2.10)

Таким образом, линии тока в любой момент представляют собой логарифмические спирали в плоскостях, ортогональных оси (Охз). Траектории же частиц описываются уравнениями (1.26) и представляют собой прямые линии.

Совпадение линий тока с траекториями происходит в двух случаях. Во-первых, это случай установившегося движения, когда поле скоростей стационарно, т. е. явно не зависит от времени:

=0 или Vi = Vi{xx,X2,X). (2.11)

в этом случае уравнения (2.3) и (2.4) идентичны. Во-вторых, такое совпадение имеет место и при неустановившемся движении, если траектории всех частиц тела прямолинейны. Тогда

проходящих через все точки квадрата и перпендикулярных в каждый момент времени отрезку 0М.

Найдём, например, линии тока для поля скоростей, задаваемого уравнениями (1.30). Подставляя (1.30) в систему (2.3), получим , , ,

dx, dx, dx, 2.5)