1U.2. Осесимметричный кольцевой элемент с треугольным поперечным сечением .

Осесимметричные сплошные элементы являются обобщением плоско-напряженных элементов и так же, как и в случае плоской деформации, здесь применимы многие построения из гл. 9. Поэтому ниже рассмотрим подробно соотношения лишь для изображенного на рис. П.З простейшего треугольного осесимметричного элемента. Элемент расположен произвольным образом в плоскости г - г так, что ни одна из сторон его не направлена вдоль оси симметрии. I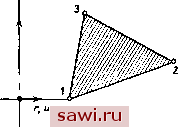

Рис. 11.3. Сечение треугольного кольцевого элемента.

Для данного типа элемента пригодно линейное поле перемещений. Так как ео находится в обратно пропорциональной зависимости от радиуса, то возникают дополнительные трудности при построении матрицы жесткости элемента даже для случая линейного поля перемещений. Чтобы понять, в чем состоят эти трудности, удобно воспользоваться обобщенными перемещениями. Поэтому выберем

u=ai-f /-f Яз 2, хю=а-\-аг-\-а,г. (П.10)

Дифференцируя эти функции в соответствии с формулами (11.4), получим

О О О 01 (ал

zir О

U[C]{a}. (11.11)

Подстановка последнего в (11.9) приводит к следующему выражению (для простоты начальные деформации исключены):

np=V2LaJ[k<l {a}-fr , (11.12)

где символом К обозначен потенциал заданных сил, выраженных через параметры {а}, а основная матрица жесткости определяется формулой

Ч[С]ЧЕ][С]гс/л1. (11.13)

(l-fti)(l-2ti)

где матрица

j[C](Ej [С] rdA имеет вид

Здесь

(11.14)

li\\rdTdz, l2=\\drdz, l\\zdrdz, (11.15-11.17) = = /,= fjfdrda. (11.18-11.20)

Величины /i, /a и / легко вычисляются. Имеем

( 1 + а + г г) У\ (гг -+ (гз - г,) + гз (г, - г,) jj jg

(11.1ба) (11.17а)

/ ki (гз -ZsJ + -j (гз -?i) + /-3(2i-2;) --2

(г! + гг + гз) [ i (гг - гз) + г (гз - г) + гз (г -

Выражения для /4, /5 и /, содержат переменную г в знаменателе и результирующие выражения имеют более сложный вид:

(11.18а) (П.19а)

где для I, /= 1,2,3

(г.-г;)

1 (riZ,~rjZi

. = тйЦг[МЗл,-л/,-.,(Зл-М]+у(; 1п,

(11.21)

и /e = Gn + G23 + G , (11.20а)

где для I, / = 1, 2, 3

+ 2г,.г(2.5л;-11г + 2 5л.) +

1 ( nzr-rjZiY fi

(11.22)

Выписанные выражения относятся к обобщенным параметрам {а}. Матрица жесткости, соответствующая физическим координатам, легко строится с помощью задания преобразования от обобщенных координат к физическим (11.10) и применения этого преобразования к [к ].

Если узлы расположены на оси симметрии, то возникают особые случаи, так как члены с In (ri/rj) и (ri-rj) в знаменателе принимают бесконечное значение. Используя правило Лопиталя, можно провести оценки. Для особого случая с г/=0, rj, гфО имеем (i, /, k- 1. 2. 3)

/, = v/[(2-2,)(3z, + г,.) + (г,-2,) (Зг, + г,)]-

(11.18Ь)

-V,2?In, (11.19b)

(11г?-Ь5г,г,-Ь22)--2?1п. (11.20b) isrii а

Заметим также, что ы,=0 приводит к уменьшению размерности матрицы жесткости.

Если Г1=Г]=0 и гФО, то можно также показать [11.3], что члены, содержащие h, /, и 1, не входят в выражение для матрицы жесткости из-за выполнения равенства Ui=U]=0.

В некоторых приложениях полезно иметь граничный элемент для сплошного цилиндра, как показано на рис. 11.4. Чтобы по-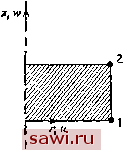

Рис. 11.4. Граничный элемент для сплошного цилиндра.

строить такой элемент, можно использовать поля перемещений и= = 0x+022 iiwasr+uiZ. Подробный вывод уравнений жесткости для данного элемента совпадает с изложенными выше операциями.

Очевидно, что получение явных точных выражений для коэффициентов жесткости, соответствующих осесимметричному тре-