Вклад деформаций сдвига в энергию деформации равен

\[(yj A.Gdx.

Поэтому с учетом выражения для сдвиговой деформации уу полная энергия деформации запишется в виде

= Т

1 / dw v

~djf

Теперь, если поперечное смещение w описывается обычным образом с помощью кубического полинома (см. (5.14а)), то можно записать данный интеграл для энергии деформации в дискретном виде и, минимизируя энергию деформации, получить матрицу жесткости элемента. Типичный член этой матрицы кц, который связывает Fz и Wi, имеет вид

, 12£/ , 144 (£ /) 11 - + А GL

Это выражение, вообще говоря, некорректно по причинам, высказанным ранее.

Простой подход к формулировке корректной матрицы жесткости элемента [12.501 состоит в том, что сначала строят матрицу податливости, учитывающую сдвиговые деформации. Так, если элемент консольно закреплен в точке 2, то смещение в точке 1, вызванное одним лишь сдвигом, равно (с G=£/2(l-f р.))

, 2(1 + ц) FiZ. --ш

и полные уравнения податливости имеют вид

Применяя методику, описанную в разд. 2.6, на основе этих уравнений строят матрицу жесткости. Тогда корректное выражение для коэффициента жесткости имеет вид

12£/ 1

Z.3 [(1 + 12(1 +ц)/)/л,Z.

Из сказанного можно сделать общий вывод, что учитывать эффекты, связанные с деформацией сдвига для балочных, пластинчатых и оболочечных элементов, можно тогда, когда они формулируются непосредственно в терминах соотношений податливости (подход на основе принципа минимума дополнительной работы)

ИЛИ в виде смешанных соотношений, получаемых из функционалов, в которые входит дополнительная энергия деформации (например, из функционала Рейсснера (12.24)).

Ранее подчеркивалось, что на практике в основном используют подходы, основанные на принципе минимума потенциальной энергии (предполагаемые перемещения). Имеется все же возможность использовать эти подходы при формулировке уравнений жесткости с учетом поперечных сдвиговых деформаций для балок, пластин и оболочек путем простой аппроксимации, в которой суммируются результаты, полученные по отдельности при анализе чистого изгиба и чистого сдвига. Чтобы описать этот подход, изучим элемент 1-2, изображенный на рис. 12.16, являющийся частью всей балочной конструкции. Из рисунка видно, что поперечная сдвиговая деформация равна yxz={wl-wl)/L, где верхним индексом s отмечено, что соответствующие перемещения обусловлены лишь деформациями сдвига. Кроме того, так как yxz=2{l+\i)Fi/AsE, то

Это - уравнение жесткости для элемента. Аналогично можно построить уравнение жесткости для оставшейся поперечной перерезывающей силы Fj. Объединяя эти уравнения жесткости обычным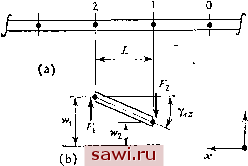

Рис. 12.16. Смещение в виде чистого сл,вига для балочного элемента, (а) Целая балка; (Ь) характер смещения для элемента 1-2.

способом, принятым в прямом жесткостном анализе, можно построить глобальные уравнения жесткости для перерезывающих сил. Обозначим их через

{Р}=[к1{А}. (12-46)

Разрешая эти уравнения, получим

{Д}=[к1-ЧР}. (12.47)

12.5. Исключение ограничения на деформации поперечного сдвига (дискретная процедура, основанная на гипотезе Кирхгофа) [12.58]

Как отмечалось, исключение деформаций поперечного сдвига при анализе изгибаемых балок и пластин осуществляется введением условия, соответствующего гипотезе Кирхгофа. Можно построить выражение для энергии деформации, не привлекая этого предположения. В этом случае можно добавить выражение для энергии сдвиговых деформаций и использовать полученное таким образом выражение для энергии при формулировке матрицы жесткости элемента.

Чтобы проиллюстрировать эту методику, вновь рассмотрим балочный элемент. Хотя условие, заключающееся в равенстве углового смещения 6 наклону (отрицательному) нейтральной оси, исключено, условие, что плоское в недеформированном состоянии сечение остается плоским и после деформации, сохраняется. Таким образом, основной величиной, описывающей деформацию изгиба, является угол 6, причем кривизна y.=dQ/dx.

Полный наклон нейтральной оси dw/dx в этом случае обусловлен двумя факторами: угловым смещением и наклоном, вызванны.м деформацией сдвига. Сохраняя упрощающие предположения о дей-

Обозначая глобальную матрицу жесткости, соответствующую чистому изгибу через [к-], а соответствующие перемещения - через {А/}, также получим

{А/}=[кЛ-ЧР}. (12.48)

Аппроксимация полных перемещений представляется в виде суммы сдвиговых и изгибных перемещений:

{А}={А-}+{А/}. (12.49)

Чтобы применить выписанную выше схему для пластин или изгибаемых оболочечных конструкций, необходимо аналитически представить конструкцию в виде системы фиктивных балочных элементов с учетом сдвиговых деформаций. Если эта аппроксимация неадекватна, то можно использовать теорию пластин, которая учитывает поперечные деформации сдвига. Существует ряд таких теорий [12.51 -12.53], и большинство из них использовалось в конечно-элементном анализе [12.54-12.57]. Однако, вероятно, что если упрощенный подход неадекватен, то и теории пластин, учитывающие деформации поперечного сдвига, будут также неадекватными. В этом случае имеет смысл применить трехмерный анализ и пространственные элементы. Мы снова вернемся к рассмотрению этого вопроса в разд. 12.6.